Scrivo i dati del problema facendo riferimento alla seguente figura:
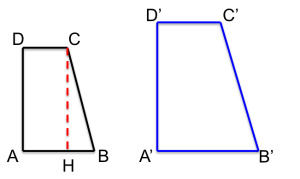
- \(\overline{AB} = 30\text{ cm};\)
- \(\overline{BC} = 50\text{ cm};\)
- \(\overline{CH} = \overline{AD} = 48\text{ cm};\)
- \(\overline{C'D'} = 24\text{ cm};\)
- I trapezi \(ABCD \) e \(A'B'C'D' \) sono simili.
CALCOLO IL SEGMENTO BH
Applico il teorema di Pitagora (il quadrato dell'ipotenusa è uguale alla somma dei quadrati dei cateti) al triangolo rettangolo BCH:
\(\overline{BH} = \sqrt{\overline{BC}^{2} - \overline{CH}^{2}}; \)
\(\overline{BC} =\sqrt{\left(50^2 - 48^2 \right)\text{ cm}^2} = \sqrt{\left(2500 + 2304\right)\text{ cm}^2} = \sqrt{106\text{ cm}^2} = 14\text{cm}. \)
CALCOLO LA BASE MINORE CD
Poichè \(\overline{AH} = \overline{CD} \), possiamo scrivere:
\(\overline{CD}=\overline{AH}=\overline{AB}-\overline{BH}=\left(30-14\right)\text{ cm}=16\text{ cm}.\)
CALCOLO PERIMETRO TRAPEZIO \(A'B'C'D' \)
Poichè i due trapezi sono simili, i lati sono in proporzione tra loro e quindi:
\(\overline{AB}:\overline{A'B'}=\overline{CD}:\overline{C'D'};\)
\(30:\overline{A'B'}=16:24 \Rightarrow \overline{A'B'}=\dfrac{30\cdot24}{16} = 45\text{ cm};\)
\(\overline{BC}:\overline{B'C'}=\overline{CD}:\overline{C'D'}\)
\(50:\overline{B'C'}=16:24 \Rightarrow \overline{B'C'}=\dfrac{50\cdot24}{16} = 75\text{ cm};\)
\(\overline{BC}:\overline{B'C'}=\overline{CD}:\overline{C'D'}\)
\(48:\overline{A'D'}=16:24 \Rightarrow \overline{A'D'}=\dfrac{48\cdot24}{16} = 72\text{ cm}; \)
A questo punto possiamo calcolare il perimetro del trapezio \(A'B'C'D' \):
\(P_{A'B'C'D'}=\overline{A'B'}+\overline{B'C'}+\overline{C'D'}+\overline{A'D'}= \left(45 + 75 + 24 + 72\right)\text{ cm} = 216\text{ cm}; \)
