Scriviamo i dati del problema facendo riferimento alla seguente figura:
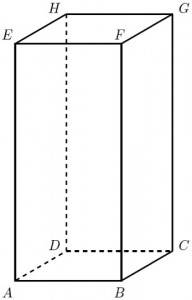
- \(h =\overline{AE} = 13,4\text{ dm}; \)
- \(\overline{AD} = 10,1\text{ dm}; \)
- \(\overline{AB} = 12,6\text{ dm}; \)
L'area totale del prisma si ottiene sommando l'area laterale e il doppio dell'area di base, cioè:
\(A_{totale} = A_{laterale} + 2 \cdot A_{base}. \)
CALCOLO AREA LATERALE
L'area della superficie laterale del prisma retto si ottiene moltiplicando il perimetro di base (\(P_{ABCD}\)) per l'altezza (h). L'altezza la conosciamo, mentre il perimetro di base possiamo calcolarlo utilizzando i dati (2) e (3) del problema:
\(P_{ABCD} = 2\cdot\overline{AB} + 2\cdot\overline{AD}; \)
\(P_{ABCD} = 2\cdot 12,6\text{ dm} + 2\cdot 10,1\text{ dm} = (25,2 + 20,2)\text{ dm} = 45,4\text{ dm}. \)
A questo punto possiamo calcolare l'area laterale del prisma e l'area della base:
\(A_{laterale} = P_{ABCD} \cdot h = 45,4\text{ dm} \cdot 13,4\text{ dm} = 608,36\text{ dm}^{2}. \)
CALCOLO AREA DI BASE
\(A_{base} = \overline{AB} \cdot \overline{AD} = \left(12,6 \cdot 10,1\right)\text{ dm}^2 = 127,26\text{ dm}^2.\)
CALCOLO AREA TOTALE
L'area totale del prisma è:
\(A_{totale} = A_{laterale} + 2 \cdot A_{base} = 608,36\text{ dm}^{2} + 2 \cdot 127,26\text{ dm}^{2} = 862,88\text{ dm}^{2} .\)
