Scriviamo i dati del problema facendo riferimento alla seguente figura:
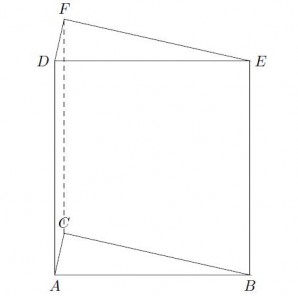
- \(A\hat{C}B = D\hat{F}E=90^{\circ}; \)
- \(A_{base} =34,56\text{ dm}^2; \)
- \({AC} = 7,2\text{dm};\)
- \(\overline{AD} = \dfrac{2}{3}\overline{AB};\)
utilizzando questi dati dobbiamo calcolare l'area laterale (\(A_{laterale}\)) del prisma. Per poter calcolare l'area laterale del prisma è necessario conoscere il perimetro del triangolo di base e l'altezza del prisma.
CALCOLO PERIMETRO DEL TRIANGOLO DI BASE
Ricordiamo che l'area di un triangolo rettangolo può essere calcolata moltiplicando i due cateti e poi dividendo per 2, cioè:
\(A_{base}=\dfrac{\overline{AC}\cdot\overline{BC}}{2};\)
da cui si ricava la seguente formula inversa per poter calcolare il cateto \(\overline{BC}\):
\(\overline{BC}=\dfrac{2\cdot A_{base}}{AC}=\dfrac{2\cdot 34,56\text{ dm}^2}{7,2\text{ dm}}=9,6\text{ dm}.\)
Applicando il teorema di Pitagora (il quadrato dell'ipotenusa è uguale alla somma dei quadrati dei cateti) al triangolo rettangolo \(ABC\) possiamo calcolare l'ipotenusa \(\overline{AB}\):
\(\overline{AB} = \sqrt{\overline{AC}^{2} + \overline{BC}^{2}}; \)
\(\overline{AB} = \sqrt{\left(7,2^{2} + 9,6^{2}\right)\text{ dm}^2};\)
\(\overline{AB} = \sqrt{\left(51,84 + 92,16\right)\text{ dm}^2} =\sqrt{144\text{ dm}^2} = 12\text{ dm};\)
\(\overline{AB} = 12\text{ dm}.\)
Il perimetro del triangolo \(ABC\) è:
\(P_{ABC} = \overline{AB} + \overline{BC} + \overline{AC} = \left(12 + 9,6 + 7,2\right)\text{ dm} = 28,8\text{ dm}. \)
CALCOLO AREA LATERALE PRISMA
Adesso calcoliamo l'altezza del prisma utilizzando il dato 4:
\(\overline{AD} = \dfrac{2}{3}\overline{AB} = \dfrac{2}{3}\cdot12\text{ dm} = 8\text{ dm}.\)
Per calcolare l'area laterale del prisma bisogna moltiplicare il perimetro del triangolo \(ABC\) per l'altezza del prisma:
\(A_{laterale} = P_{ABC}\cdot\overline{AD} = \left(28,8\cdot 8\right)\text{ dm}^{2} = 230,4\text{ dm}^{2}. \)
