Matematica

Scriviamo i dati facendo riferimento alla seguente figura:

1. $AC=26\text{ m};$
2. $BC=19,5\text{ m};$
3. $A\hat{C}B={90}^{\circ };$

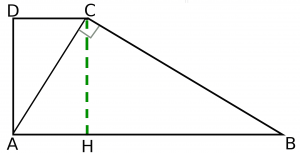
CALCOLO BASE MAGGIORE $AB$

La base maggiore $AB$ può essere calcolata applicando il teorema di Pitagora (il quadrato dell'ipotenusa è uguale alla somma dei quadrati dei cateti) al triangolo rettangolo $ABC$:

$AB=\sqrt{A{C}^2+B{C}^2}=\sqrt{({26}^2+19,5^2){\text{ m}}^2}=\sqrt{(676+380,25){\text{ m}}^2}=32,5\text{ m}.$

CALCOLO $AH$ (proiezione del cateto $AC$ sull'ipotenusa $AB$)

Per calcolare $AH$ applico il primo teorema di Euclide (in un triangolo rettangolo un cateto è medio proporzionale tra l'ipotenusa e la proiezione del cateto stesso sull'ipotenusa) al triangolo rettangolo $ABC$. Nel nostro caso il cateto considerato è $AC$, mentre la sua proiezione sull'ipotenusa è $AH$, quindi possiamo scrivere che:

$AB:AC=AC:AH\Rightarrow AH={\displaystyle \frac{A{C}^2}{AB}}={\displaystyle \frac{{\left(26\text{ m}\right)}^2}{32,5\text{ m}}}={\displaystyle \frac{676{\text{ m}}^2}{32,5\text{ m}}}=20,8\text{ m}.$

Per costruzione sappiamo che $CD=AH=20,8\text{ m}$.

CALCOLO  ALTEZZA $CH$

Per poter calcolare $CH$ è necessario conoscere prima il segmento $BH$ che può essere calcolato facilmente sottraendo all'ipotenusa $AB$ il segmento $AH$:

$BH=AB-AH=(32,5-20,8)\text{ m}=11,7\text{ m}.$

Per calcolare $CH$ applico il secondo teorema di Euclide (in un triangolo rettangolo l'altezza relativa all'ipotenusa  è medio proporzionale tra le proiezioni dei due cateti sull'ipotenusa) al triangolo rettangolo $ABC$. Nel nostro caso le proiezioni dei cateti sull'ipotenusa sono $AH$ e $BH$, quindi possiamo scrivere che:

$AH:CH=CH:BH\Rightarrow C{H}^2=AH\cdot BH;$

$CH=\sqrt{AH\cdot BH}=\sqrt{(20,8\cdot 11,7){\text{ m}}^2}=15,6\text{ m}$.

Per costruzione sappiamo che $AD=CH=15,6\text{ m}.$

CALCOLO  PERIMETRO TRAPEZIO

Adesso abbiamo tutti i dati necessari per calcolare il perimetro del trapezio $ABCD$:

$P_{ABCD}=AB+BC+CD+AD=(32,5+19,5+20,8+15,6)\text{ m}=88,4\text{ m}.$