Matematica

C'è un punto della traccia non molto chiaro quando dice che l'R del prisma è 12 cm. Tuttavia analizzando bene il problema credo che R sia l'altezza del prisma altimenti il problema non è risolvibilie. Quindi supponendo che sia così procediamo nel seguente modo. Scriviamo i dati del problema facendo riferimento alla seguente figura:

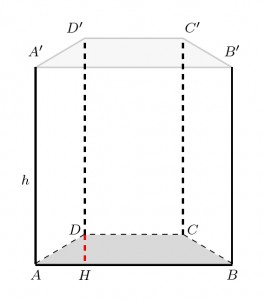
1. \(h = 12\text{ cm}\) (altezza prisma);
2. \(AB =11\text{ cm} \) (base maggiore trapezio);
3. \(CD = 8\text{ cm}\) (base minore trapezio);
4. \(AD = BC = 5\text{ cm}\) (lato obliquo trapezio);

CALCOLO ALTEZZA DH DEL TRAPEZIO DI BASE

In un trapezio isoscele il segmento \(AH\) è uguale alla differenza delle basi diviso 2:

\(AH = \dfrac{AB - CD}{2} = \dfrac{(11-8)\text{ cm}}{2} = 1.5\text{ cm}.\)

Applicando il teorema di Pitagora al triangolo \(ADH\) posso calcolare l'altezza \(DH\):

\(DH = \sqrt{AD^2 - AH^2}\);

\(DH=\sqrt{\left(5^2 - 1.5^2\right)\text{ cm}^2} = \sqrt{\left(22,75\right)\text{ cm}^2} = 4.769696\text{ cm}.\).

CALCOLO AREA DI BASE (area trapezio)

L'area del trapezio di base si calcola nel seguente modo:

\(A_{trapezio} = \dfrac{\left( AB + CD \right) \cdot DH}{2};\)

\(A_{trapezio}=\dfrac{\left( 11\text{ cm} + 8\text{ cm} \right)\cdot 4.769696\text{ cm}}{2} = 45.312112\text{ cm}^2.\)

CALCOLO AREA LATERALE

L'area laterale di un prisma  retto si calcola moltiplicando il perimetro della base per l'altezza del trapezio:

\(A_{laterale} = P_{trapezio}\cdot h\)

\(P_{trapezio} = AB + BC + CD + AD = \left(11 + 5 + 8 + 5\right)\text{ cm} = 29\text{ cm}.\)

\(A_{laterale} = P_{trapezio}\cdot h = \left(29\cdot 12\right)\text{ cm}^2 = 348\text{ cm}^2.\)

CALCOLO AREA TOTALE

\(A_{tot} = A_{laterale} + 2\cdot A_{trapezio} = \left(348 + 2\cdot 45.312112\right)\text{ cm}^2 = 438,624224\text{ cm}^2. \)