Scriviamo i dati del problema facendo riferimento alla seguente figura:
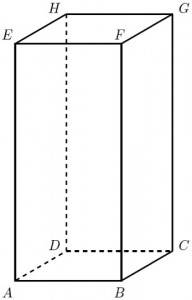
- \(h=AE=36\text{ cm}\);
- \(A_{base} = 360\text{ cm}^2; \)
- \(\overline{AD} = \dfrac{5}{8}AB\).
CALCOLO PERIMETRO DI BASE
La base del prisma è un rettangolo quindi la sua area si calcola moltiplicando i due lati \(AD\) e \(AB\)
\(A_{base} = AD\cdot AB = \dfrac{5}{8}AB\cdot AB = \dfrac{5}{8}AB^2\).
Utilizzando il dato 2 possiamo scrivere la seguente equazione:
\(A_{base} = \dfrac{5}{8}AB^2 = 360\text{ cm}^2 \Rightarrow AB = 24\text{ cm}\).
Utilizzando il dato 3:
\(\overline{AD} = \dfrac{5}{8}AB = \dfrac{5}{8}24\text{ cm} = 15\text{ cm}\).
Pertanto, il perimetro di base è:
\(P_{ABCD} = 2\cdot\overline{AB} + 2\cdot\overline{AD} =(2\cdot24 +2\cdot 15)\text{ cm} = 78\text{ cm}\).
CALCOLO AREA LATERALE
L'area della superficie laterale del prisma retto si ottiene moltiplicando il perimetro di base (\(P_{base}\)) per l'altezza (h):
\(A_{laterale} = P_{ABCD} \cdot h = 78\text{ dm} \cdot 36\text{ cm} = 2808\text{ cm}^{2}. \)
CALCOLO AREA TOTALE
L'area totale del prisma è:
\(A_{totale} = A_{laterale} + 2 \cdot A_{base} = 2808\text{ cm}^{2} + 2 \cdot 360\text{ cm}^{2} = 3528\text{ cm}^{2} .\)
