Matematica

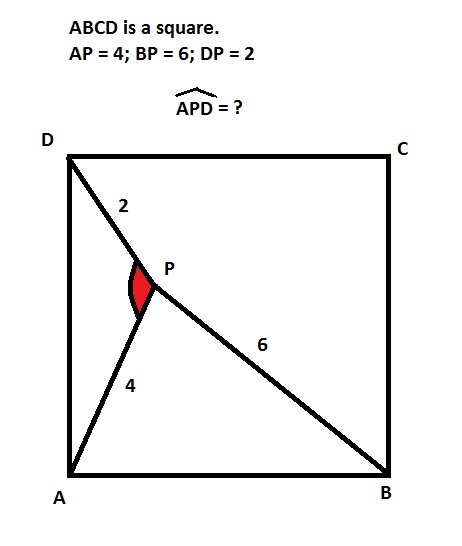
Per calcolare l'angolo \(\hat{APD} \) puoi procedere nel seguente modo:

indichaimo con \(x\) l'altezza del triangolo APD e con \(y\) l'altezza del triangolo APB. Infine indichiamo con \(a\) il lato del quadrato come riportato nella seguente figura:

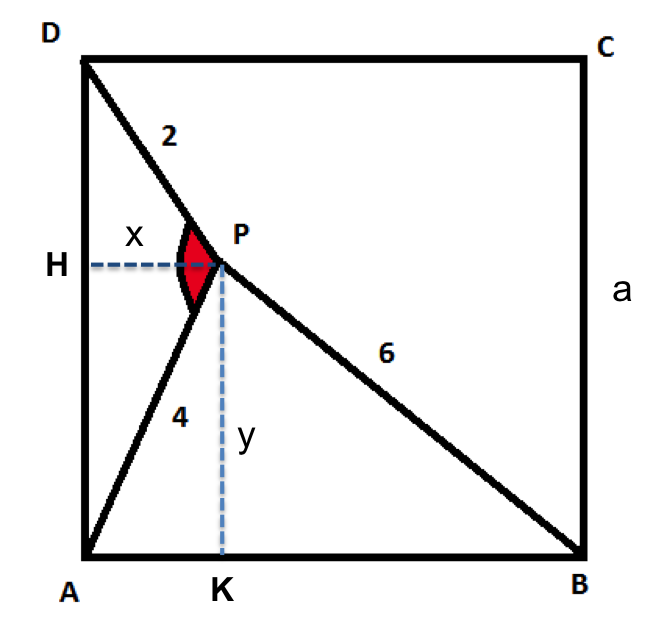
Applico il teorema di Pitagora al triangolo \(PDH\):

\(DH^2 + PH^2 = PD^2 \Rightarrow (a-y)^2 + x^2 = 4; \)

Applico il teorema di Pitagora al triangolo \(PAH\):

\(PH^2 + AH^2 = PA^2 \Rightarrow x^2 + y^2 = 16; \)

Applico il teorema di Pitagora al triangolo \(PBK\):

\(PK^2 + BK^2 = P B^2 \Rightarrow y^2 + (a-x)^2 = 36; \)

In questo modo abbiamo un sistema di tre equazioni in tre incognite \(x,y,a\), che possimao risolvere facilmente trovando il valore del lato del quadrato. Più precisamente possiamo trovare che:

\(a^2 = 20 \pm 8\sqrt{2}\)

A questo punto possiamo applicare il teorema di Carnot al triangolo \(APD\) e trovare l'angolo \(\hat{APD}\) che più semplicemente denotiamo con \(\alpha\) :

\(a^2 = PD^2 + PA^2 - 2\cdot PD\cdot PA\cdot \cos(\alpha)\)

risolvendo questa equazione si ottengono due possibili soluzioni: \(\alpha = 45°\) oppure \(\alpha = 135°\).