In un triangolo rettangolo è inscritta una circonferenza . Il punto in cui tale circonferenza tocca l'ipotenusa la divide in due segmenti il cui prodotto è 11. Calcolare l'area del triangolo rettangolo. ( Vorrei sapere il procedimento , grazie .
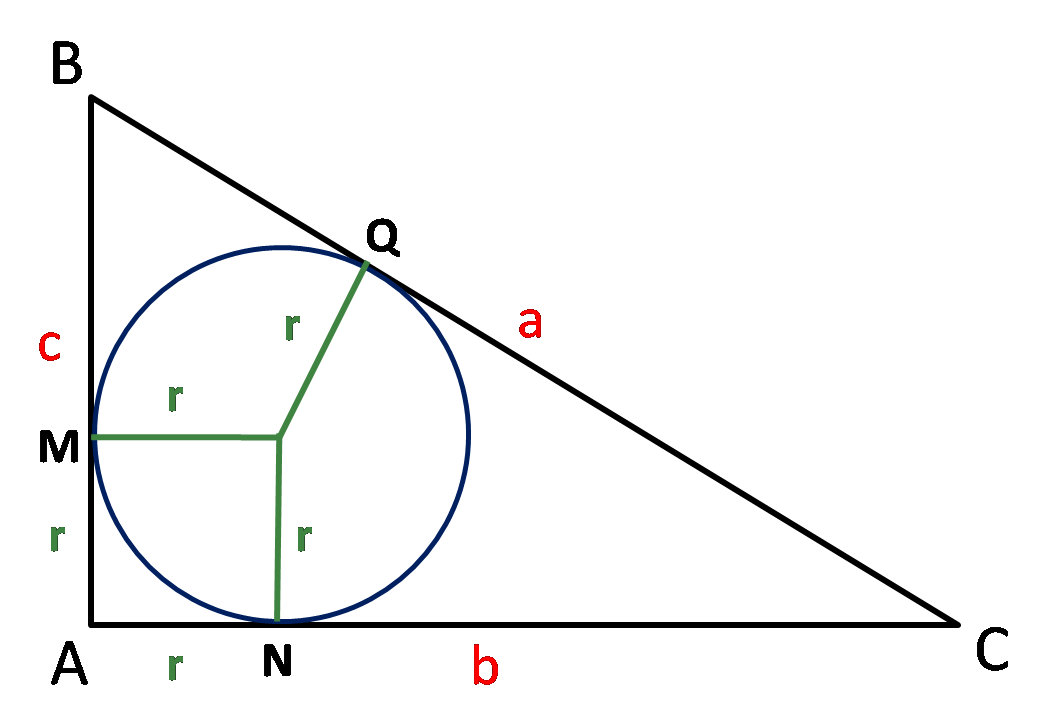
Ciao Greena, facendo riferimento alla figura sottostante ti mostrerò come risolvere il problema.
Dalla traccia sappiamo che \(BQ\cdot QC = 11\) .
Per semplicità indichiamo con \(a\),\(b\) e \(c\) l'ipotenusa e i due cateti del triangolo rettangolo.
Per costruzione sappiamo anche che \(AM = AN = r\), dove \(r\) è il raggio del cerchio.
Per le proprietà delle tangenti da un punto esterno si ha che:
\(QC = NC = b-r;\)
\(BQ = BM = c-r;\)
Pertanto possiamo scrivere:
\(BQ \cdot QC = (b-r)\cdot(c-r) = b\cdot c -b\cdot r-c\cdot r+r^2=11\). (eq. 1)
Inoltre, sommando i due segmenti che costituiscono l'ipotenusa si ha che:
\(a = BQ+QC=b+c-2r\);
Calcoliamo adesso il semiperimetro del triangolo rettangolo che indichiamo con \(P\)
\(P = \dfrac{a+b+c}{2} =\dfrac {b+c-2r+b+c}{2} = b+c-r\)
Ricordando la relazione che lega l'area (\(S\)), il raggio (\(r\)) della circonferenza inscritta ed il semiperimetro di un triangolo, possiamo scrivere:
\(S = r\cdot P = r\cdot(b+c-r) = b\cdot r + c\cdot r - r^2\)
Inoltre sappiamo anche che:
\(b\cdot c = 2S\)
Sostituendo queste due relazioni in (eq. 1) si ha che:
\(2S - S = 11 \Rightarrow S = 11.\)
