Un triangolo ABC inscritto nella semicirconferenza (BC=diametro), presenta un lato AB pari a 76 m, ed il relativo cateto AH (altezza del triangolo ABC, H incidente su BC e non coincidente con il centro del cerchio) pari a 60,8m.
Trovare area del semicerchio e del triangolo.
Help!!!
Grazie...
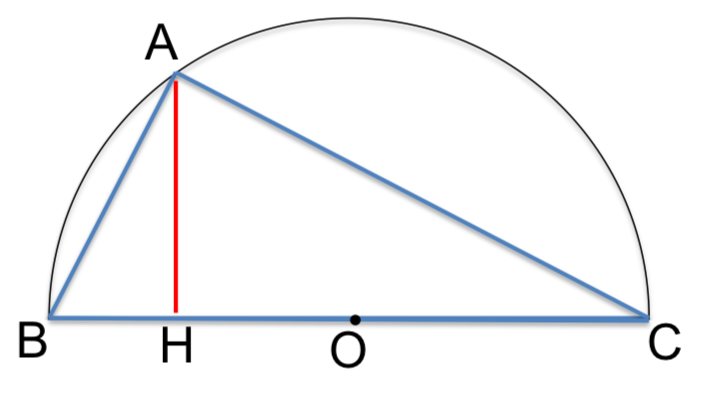
Indicato con \(O\) il centro della semicirconferenza, si ha :
\(BH\) lo possiamo trovare applicando il teorema di Pitagora
\(BH = \sqrt{76^2 - 60,8^2}=45,6\;m\)
Con il 2° teorema di Euclide ci troviamo \(HC\)
\(HC = \dfrac{60,8^2}{45,6} = 81,06\;m\) .
A questo punto abbiamo \(BC\) sommando \(BH\) e \(HC\)
\(BC = BH+HC = 45,6 + 81,06 = 126,66\;m\),
che è anche il diametro del semicerchio e la base del triangolo rettangolo.
Possiamo finalmente calcolare l'area del triangolo:
\(\dfrac{BC\cdot AH}{2} = \dfrac{126,66\cdot60,8}{2} = 3850,464\;m^2\).
Ed infine l'area del semicerchio:
\( \dfrac{ raggio^2 \cdot \pi }{ 2} = \dfrac{OC^2 \cdot \pi }{2} = \dfrac{63,33 \cdot 63,33 \cdot \pi}{2} = 2005,34 \cdot \pi \; m^2. \)
NOTA :
1) In ogni semicirconferenza è inscritto sempre e solo un triangolo rettangolo .
2) L'area di un cerchio si calcola facendo raggio × raggio × pi greco , con pi greco = circa 3,14 . Per cui l'area di una semicirconferenza è la metà dell 'area di un cerchio .
Spero che sia stata chiara e di aiuto . Ciao