Problema di trigonometria Triangolo qualunque
Sia ABC un triangolo qualunque. Si tracci l'altezza BH affinché l'angolo ABH sia 1/3 dell'angolo HBC. Si sa, inoltre, che AB misura k, BC misura 4k, l'area di ABH è uguale ad 1. Calcolare l'area di BHC.
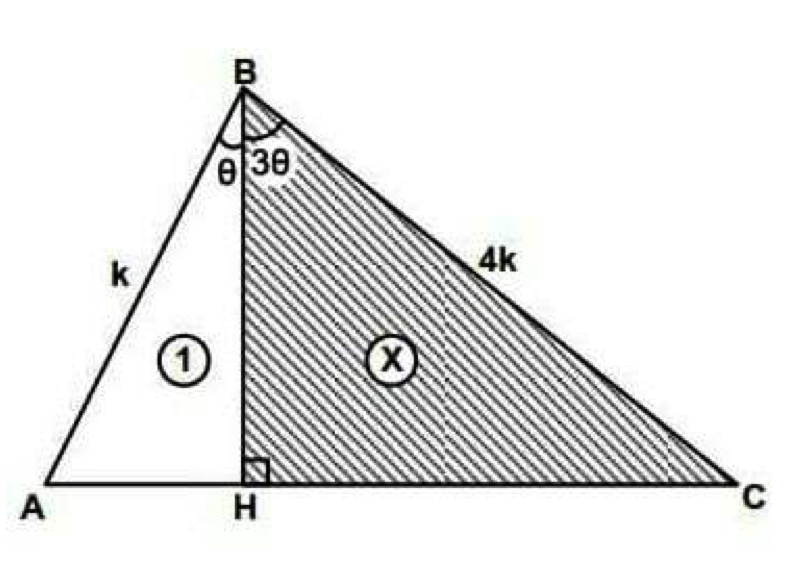
Sia ABC un triangolo qualunque. Si tracci l'altezza BH affinché l'angolo ABH sia 1/3 dell'angolo HBC. Si sa, inoltre, che AB misura k, BC misura 4k, l'area di ABH è uguale ad 1. Calcolare l'area di BHC.

Applico il teorema del seno ai triangoli ABH e BHC per trovare BH:
\(BH:\cos(\alpha) = k:1 \rightarrow BH = k\cdot \cos(\alpha)\) (1),
\(BH:\cos(3\alpha) = 4k:1 \rightarrow BH = 4k\cdot \cos(3\alpha)\) (2).
Eguagliando la (1) e la (2), si ha:
\(cos(\alpha) = \dfrac{\sqrt{13}}{4}\) e \(sen(\alpha) = \dfrac{\sqrt{3}}{4}\).
Di seguito riporto i passaggi effettuati:
\(4k\cdot \cos(3\alpha) = k\cdot \cos(\alpha)\);
\(4\cdot \cos(\alpha + 2\alpha) = \cos(\alpha)\);
\(4\cdot (\cos(\alpha)cos(2\alpha) - \sin(\alpha)\sin(2\alpha) ) = \cos{\alpha}\);
\(4 \cos(\alpha)[\cos^2(\alpha)-\sin^2(\alpha)] - 4\sin(\alpha)\cos(\alpha)\cdot2\sin(\alpha) = \cos{\alpha}\);
\(4\cos^3(\alpha) - 4\cos(\alpha)\sin^2(\alpha) - 8\sin^2(\alpha)\cos(\alpha) = \cos(\alpha)\);
divido per \(\cos(\alpha)\) : \(4\cos^2(\alpha) - 4\sin^2(\alpha) - 8\sin^2(\alpha) = 1\);
\(4(1-\sin^2(\alpha)) -12\sin^2(\alpha) =1;\)
\(4-16\sin^2(\alpha) =1;\)
\(\sin^2(\alpha) =\dfrac{3}{16} \Rightarrow \sin(\alpha)=\dfrac{\sqrt{3}}{4}; \cos(\alpha) = \dfrac{\sqrt{13}}{4}\).
Calcolo l'area di ABH applicando la formula del seno:
\(A_{ABH}=\dfrac{k^2\sin(\alpha)\cos(\alpha)}{2}\)
Dai dati so che tale area è uguale a 1. Eguagliando tale area a 1 e mettendo in essa i valori di \(\sin(\alpha)\) e \(\cos(\alpha)\) trovati, ottengo:
\(k^2 = \dfrac{32}{\sqrt{39}}.\)
Calcolo l'area di BHC, utilizzando la formula del seno:
\(A_{BHC} = \dfrac{16k^2\cos(3\alpha)\cdot\sin(3\alpha)}{2}\) (3), oppure
\(A_{BHC} = \dfrac{k\cos(\alpha)\cdot4k\cdot\sin(3\alpha)}{2}\) (4).
L'espressione (4) è più agevole, quindi la prenderò in considerazione. Sapendo che
\(\sin(3\alpha) = \sin(2\alpha + \alpha) = \sin(\alpha)\cos(2\alpha) + sin(2\alpha)\cos(\alpha) =\)
\(= [\sin(\alpha)(\cos^2(\alpha)-\sin^2(\alpha))+2\sin(\alpha)\cos^2(\alpha)]\)
basta andare a sostituire nella (4) tale valore, poi sostituire i valori di k , \(\sin(\alpha)\), \(\cos(\alpha)\) trovati, per ottenere che:
\(A_{BHC} = 9\).
Spero di essere stata chiara. Mi farebbe molto piacere ricevere una risposta da te per sapere se ti sono stata di aiuto. Ciao