Matematica

Prima di mostrarti il procedimento, è d'obbligo fare una premessa relativa alla Geometria elementare:  

se da un punto P, esterno ad una circonferenza, tracciamo le due tangenti alla circonferenza, i segmenti di tangenza avranno la stessa lunghezza.

Detto ciò, passo allo SVOLGIMENTO del tuo PROBLEMA.

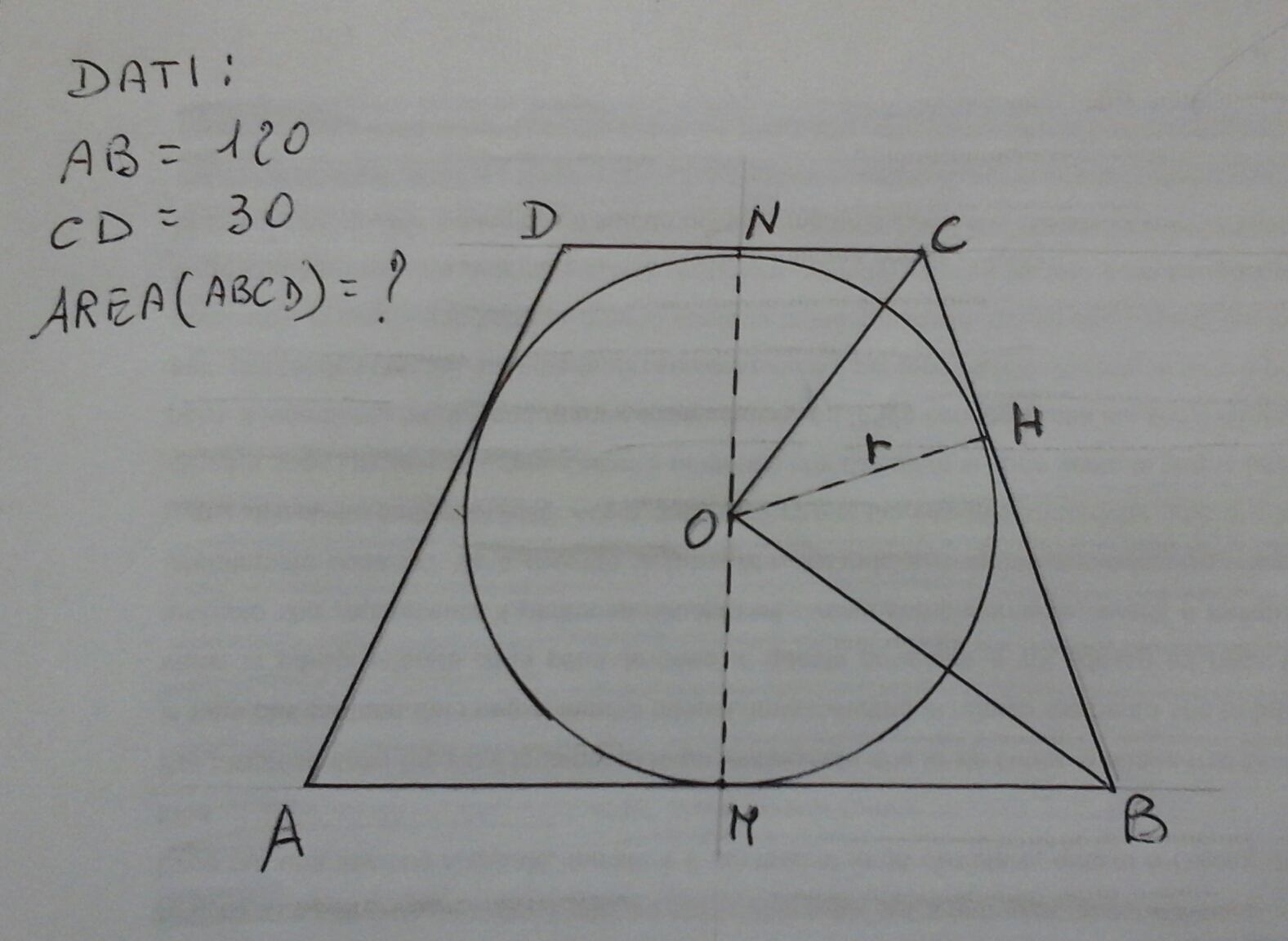
In un trapezio isoscele circoscritto ad una circonferenza, si può facilmente dimostrare che l'angolo  COB è di  90°, per cui il triangolo  COB è retto.

Il segmento  NM, oltre ad essere il diametro della circonferenza, divide a metà la base minore e la base maggiore.

OH è il raggio e altezza reativa al'ipotenusa  BC.

Dalla premessa fatta, si deduce che:

\(BH = BM = \dfrac{AB}{2} = \dfrac{120}{2} = 60.\)

\(CH = CN = \dfrac{DC}{2} = \dfrac{30}{2} = 15.\)

Applicando il  2° Teorema di Euclide (l'altezza relativa all'ipotenusa è medio proporzionale alle proiezioni dei cateti sull'ipotenusa) al triangolo rettangolo COB possiamo calcolare l'altezza relativa all'ipotenusa OH, che è anche il raggio della circonferenza:

\(OH^2 = CH\cdot BH \Rightarrow OH = \sqrt{15\cdot 60} = 30\) . 

Conoscendo il raggio OH si calcola facilmente il diametro:

\(NM = OH\cdot 2 = 30 \cdot 2 = 60;\)

A questo punto abbiamo tutti i dati per calcolare l'area del nostro trapezio isoscele: 

\(Area = \dfrac{(AB + CD)\cdot NM}{2} = \dfrac{(30 + 120)\cdot 60}{2} = 4500 \;cm^2\)

Spero ti sia stata di aiuto.   Ciao