Problema Triangolo isoscele angoli
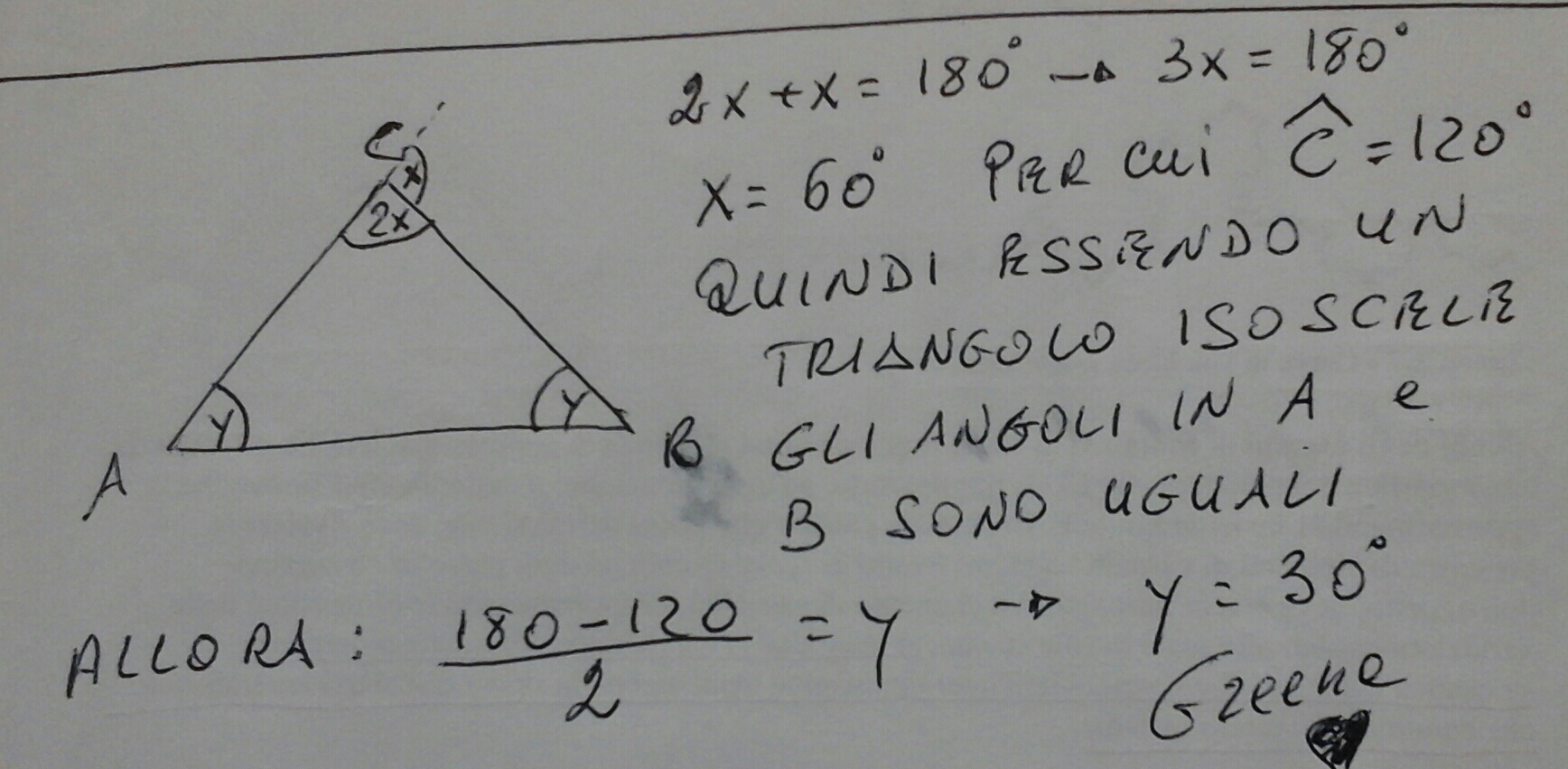
In un triangolo isoscele l'angolo al vertice è doppio del suo angolo esterno. calcola l'ampiezza degli angoli alla base.
Ricompensa per la miglior risposta: 1 moneta 
La somma degli angoli interni di un triangolo è 180°. Poiché un triangolo isoscele ha gli angoli alla base congruenti, allora possiamo scrivere che (vedi Figura):
(1) 2*a + b = 180°
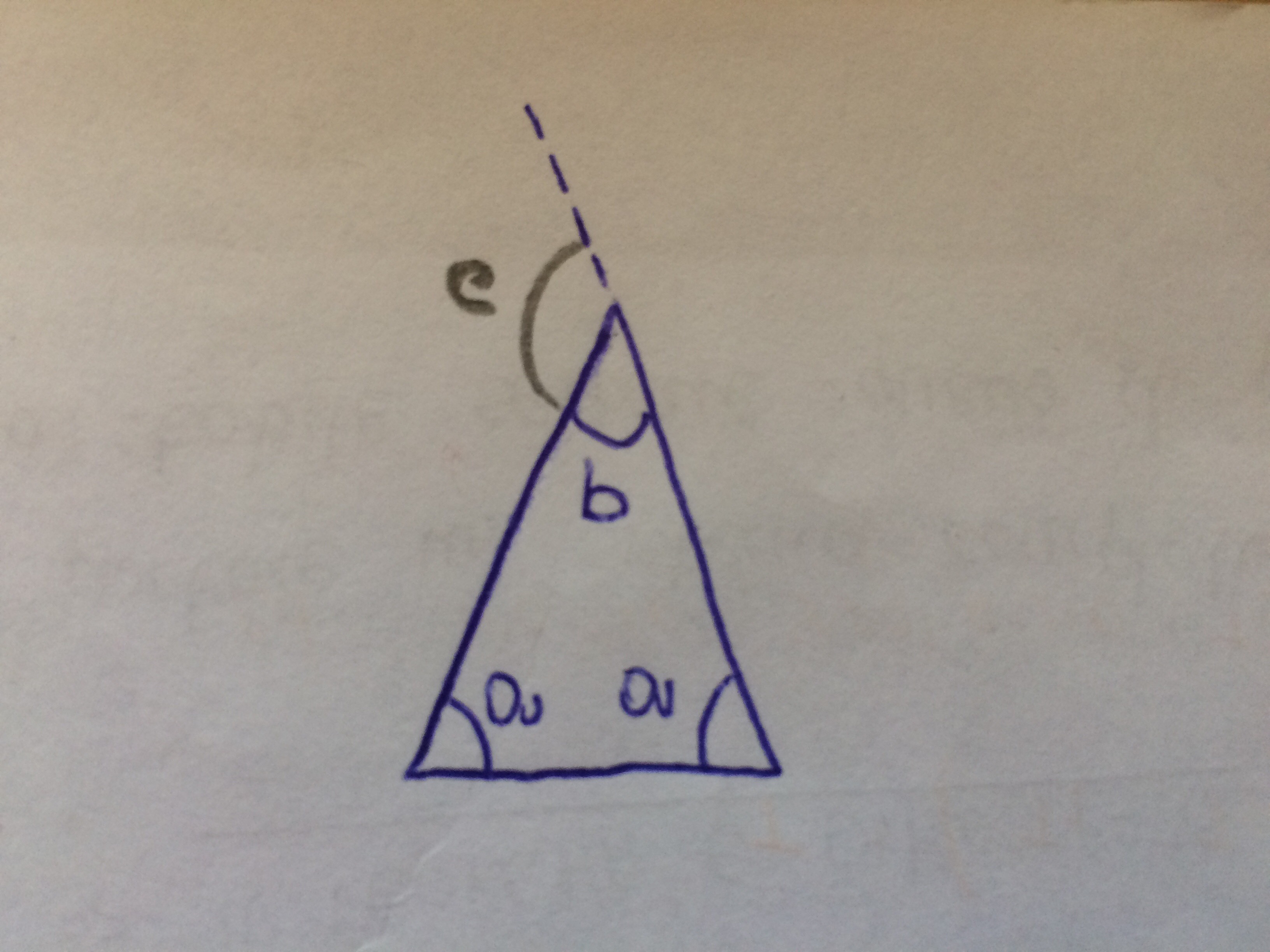
L’angolo al vertice b è il doppio dell’angolo esterno c, ovvero:
(2) b = 2*c
Per il secondo teorema dell’angolo esterno (“In ogni triangolo, l’angolo esterno è congruente alla somma degli angoli interni non adiacenti ad esso”), vale che:
(3) c = a+a = 2*a
Sostituiamo c nell’espressione (2) e otteniamo:
(4) b = 2*(2*a) = 4*a
A questo punto, sostituiamo l'espressione di b ottenuta nella (4) all'interno della (1):
2*a + 4*a = 180° —> 6*a = 180° —> a= 180°/6 —> a=30°.
Per cui l’ampiezza di ciascun angolo alla base del triangolo isoscele è 30°.
