1. Un angolo alla circonferenza e il corrispondente angolo al centro sono complementari. Qual'è l'ampiezza dei due angoli?
2.Un angolo alla circonferenza e il corrispondente angolo al centro sono supplementari. Qual'è l'ampiezza dei due angoli?
Ciao, occorre considerare la relazione tra angoli al centro e angoli alla circonferenza.
Dato un angolo alla circonferenza, si dice angolo al centro corrispondente l’angolo che ha il vertice nel centro della circonferenza e che insiste sullo stesso arco.
Vedi Immagine, dove a = angolo alla circonferenza ed insiste su AB, b = angolo al centro corrispondente ad a.
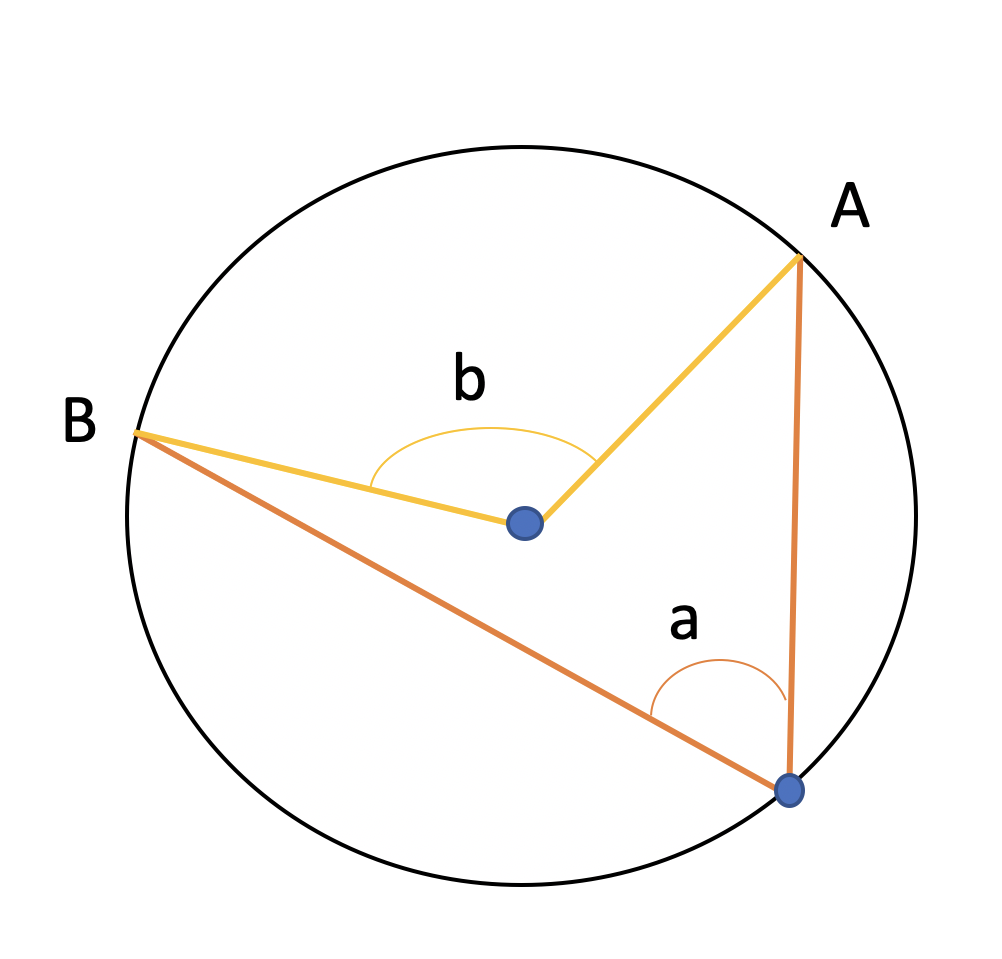
Inoltre vale il seguente teorema: un angolo alla circonferenza è la metà del suo angolo al centro corrispondente, cioè
\(a = \dfrac{b}{2} \) (1).
1. Nel primo quesito, l'angolo alla circonferenza e l'angolo al centro corrispondente sono complementari, ciò vuol dire che la loro somma è 90°:
\(a + b = 90°\) (2).
Per il teorema sopra riportato, possiamo sostituire nella (2) la formula di a (cioè la (1)), ottenendo:
\(\dfrac{b}{2} + b = 90°;\)
\( \dfrac{3}{2} b = 90° \Rightarrow b = \dfrac{2 \cdot 90°}{3} = 60°\)
Sostituiamo il valore di b = 60° appena trovato nell'espressione di a, ottenendo:
\(a = \dfrac{60}{2} = 30°\).
2. Nel secondo quesito, l'angolo alla circonferenza e l'angolo al centro corrispondente sono supplementari, ciò vuol dire che la loro somma è 180°:
\(a + b = 180°\) (3).
Per il teorema sopra riportato, possiamo sostituire nella (3) la formula di a (cioè la (1)), ottenendo:
\(\dfrac{b}{2} + b = 180°;\)
\(\dfrac{3}{2} b = 180° \Rightarrow b= \dfrac{2 \cdot180°}{3}=120°\)
Sostituendo nell'espressione di a, otteniamo:
\(a = \dfrac{120°}{2} = 60°\).